ACL2016 Best Paper: Learn Language Games Through Interactive Learning
Learn language games interactively
Joint compilation: Zhang Min, Gao Fei, Chen Chun
Summary
We introduce a new type of language learning setup related to building adaptive natural language interfaces. It is inspired by Wittgenstein's language games: a person wants to perform a certain task (eg build some kind of building block structure) but only interacts with the computer and let the computer do the actual operation (eg move all Red building blocks). The computer is initially ignorant of the language and must learn from scratch through interactions, while humans properly adjust the performance of the computer. We created a block game called SHRDLURN and collected 100 players' interactions with the computer. First, we analyzed human strategies and found that the use of combinational models and the avoidance of homogeneity were positively correlated with task performance. Second, we compared computer strategies and found that constructing pragmatics models based on semantic analysis models can accelerate the learning process for more strategic players.
1 Introduction
Wittgenstein said a well-known saying: Language comes from the meaning of its use, and it also introduces language games to illustrate the concepts of language mobility and purpose. He described how Builder B and Assistant A used the original language (composed of "blocks," "pillars," "boards," and "beams") to successfully communicate and move blocks from A to B. This is just one of the languages; there are many languages ​​that can also accomplish the goal of cooperation.
This article explores and implements the idea of ​​language games in learning settings. We call this interactive learning through language games (ILLG). In the ILLG setting, two participants initially speak different languages, but Still need to cooperate to complete a goal. Specifically, we created a game called SHRDLURN to pay tribute to the pioneering work of Winograd. As shown in Figure 1, the goal is to convert the initial state to the target state, but the only action that a person can perform is to enter a discourse. Based on its current model, the computer analyzes the discourse and produces a list of possible understandings. Humans move from top to bottom through the list and select a predetermined state while advancing the state of the block and providing feedback to the computer. Both humans and computers want to reach the target state with as little movement as possible (the target state is only known to humans). If the computer is to succeed, it must learn human language quickly in the process of the game so that humans can accomplish their goals efficiently. On the contrary, humans must also accommodate computers, at least in part, to understand what they can and cannot do.

We simulated the computer in ILLG as a semantic analyzer (Section 3), which puts a natural language discourse map (eg, "red delete") into a logical form (eg, delete (red)). Semantic parsers do not have seed dictionary and comment logic forms, so it only produces many candidate logical forms. Based on human feedback, it performs online gradient updates on the corresponding simple lexical feature parameters.
In the process, we found that although computers can eventually learn languages, their learning speed and expectations are much worse. For example, after learning to convert deleted red to logical deletion (red), the computer will also convert the deleted cyan into logical deletion (red), and humans may use exclusivity to exclude this assumption. Therefore, we introduce a pragmatics model in which computers understand human thinking. Inspired by previous pragmatics work. In order to fit the ILLG model, we introduce a new online learning algorithm. Based on experience, we have proved that the best non-pragmatic model (Section 5.3) compared to the 10 most successful players, our pragmatic model increases the accuracy of online by 8%.
What sets ILLG apart is the real-time nature of learning, in which humans also learn and adapt to computers. Structured humans can teach computers in any language—English, Arabic, Polish, a custom programming, but good players will choose to use languages ​​that allow computers to learn faster. In communicative language theory, humans contain computers. Using Amazon Mechanical Turk, we collected and analyzed about 10k sentences from 100 games of SHRDLURN. The results show that successful players tend to use a combined statement with a consistent vocabulary and grammar, which is consistent with the perceptual prejudice of the computer (Section 5.2). In addition, through this interaction, many players adapt to computers by becoming more consistent, accurate, and concise.
In practical terms, natural language systems are often trained and deployed, and users must endure their imperfections in life. We believe that to create adaptive and customizable systems, learning ILLG settings is indispensable, especially for resources and resource-poor languages ​​(it is inevitable from near zero).
2. Settings
We now formally describe the language game interactive learning (ILLG) settings. There are two game players - humans and computers. The game is played through a fixed number of levels. In each level, both players are provided with the initial state s∈γ, but only the human player knows the final state t∈γ (for example, in SHRDLURN, γ is the set of all configurations of the block). The human sends a word X (for example, removes red) to the computer. The computer then builds a list of possible candidate actions Z = [z1, . ., zK] ⊆ Z (eg, remove(with(red)), add(with(orange)), etc.) where Z is all possible behavior. For each zi∈Z, yi=[zi]s is calculated and the state of execution of the action on state s is inherited. The computer returns an ordered list of human inheritance states Y = [Y1,. ..YK ]. The human then selects yi from the list Y (the calculation is correct if i=1). The status is then updated to s=yi. When S = T is the end of this level, and the player advances to the next level.
Since only humans know the target state t and only the computer can perform the game, to successfully play the game, humans must program the desired action in statement x. However, we assume that the two players do not have a shared language, and the use of humans must pick the language and teach the computer language. As an additional twist, humans do not know the exact action Z (although they may have some concepts about the function of the computer). Finally, humans only see the result of the computer's actions, not the actual logical actions themselves.
We expect the game to proceed as follows: In the beginning, the computer does not understand the meaning of human beings and perform arbitrary actions. When the computer gets feedback and learns, both of them should become more proficient in communicating and playing games. Our key design principle is: To achieve good game performance, players need language learning.
SHRDLURN. We now describe the specifics of the game SHRDLURN. Each state s ∈ γ consists of a stack of color blocks arranged in a row ( FIG. 1 ), where each stack is a vertical column of blocks. Action Z is defined by the grammatical components in Table 1. Each action will neither increase from the stack set, nor will it be removed, and calculate stacks and select colors through various set operations. For example, the action delete (leftmost (and (red))) deletes the red block from the leftmost stack. The combination of actions gives the computer unusual capabilities. Of course, humans must teach a language to use these capabilities, even though they do not fully know the exact degree of competence. The actual game follows the course, where early levels only require simpler actions (with fewer predicates).
We describe SHRDLURN in this way for several reasons. First, the visual block is intuitive and easy to crowdsource, and it can serve as a fun game that people can actually play. Second, the action space is designed to combine to reflect the structure of natural language. The third most action z leads to the same inheritance state y=[|z|]s. For example, in some states s, the “left stack†may coincide with the “red stack of blocksâ€, so the action involves any one of them. Both will lead to the same result. Therefore, as long as humans point out the correct Y, the computer must deal with this indirect supervision (reflecting real language learning).
3. Semantic analysis model
Following the work of Zettlemoyer and Collins and the recent semantic analysis, we used a logical loglinear model (action) z∈Z to give a discourse x:

The extension y (inheritance state) is obtained by extending z over state s; formally speaking, y=[|z|]s
Features. Our feature is the combination of n-grams (including skip-grams) and tree-grams on the logical form side. Specifically, on the side of the utterance (as in red in orange), we use one dollar ('stack', ∗, ∗), two yuan ('red', 'on', ∗), trigrams ('red', 'on ', "orange"), and skip-trigrams('stack', ∗,'on'). Logically, features correspond to predicates in logic and their arguments. For each predicate h, let hi be the i-th argument for h. Then we define the characteristics of the tree-gram for the predicate h (h, d) and the depth d = 0, 1, 2, 3 recursively as follows:
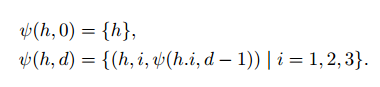
All functional collections are simply cross-products of discourse features and logical formal features. E.g

Please note that compared to most traditional semantic analysis work, we do not simulate a clear alignment or derive connected utterance components and logical forms, but follow a loose semantic model similar to (Pasupat and Liang). Because the number of derived is much greater than the number of logical forms, when we learn from the logical form of the annotation or have a seed vocabulary, modeling a definite route or derivation is the only feasible calculation. None of the ILLG settings are available.
Generate/Resolve. We use beam search to generate logical form from minimum to maximum. Specifically, for each size n = 1,.....8, we can construct a set of logical forms of size n (with n determined) in accordance with the grammar rules in Table 1 in combination with a smaller-scale logical form. predicate). For each n, we keep 100 logical form z (having the highest score θTφ(x, z)) according to the current model θ. Let Z be the set of logical forms of the final beam, which contains all n-sized logical forms.

Table 1: This formal syntax defines the composition of the action space Z for the game SHRDLURN. Use c for color and s for collection. For example, an action involved in SHRDLURN: 'add an orange block to all but the left msost brown block' add (not(leftmost(with brown))), orange). With the exception of the leftmost brown block, set the rest of the other blocks to orange.
During the training process, due to the deletion of medium-sized logical forms, there is no guarantee that Z contains logical forms that can obtain observable states y. In order to reduce this effect, we list a chart so that at the primary level we only need to use some simple actions. Before we move to a larger combo-type action, we give people the chance to give the computer some basic belongings, for example, colors. priority.
This system runs all the logical forms in the final beam search operation and sorts the final instruction result y according to the maximum probability of any logical form.
Learning When people provide feedback in the form of a specific instruction y, the system generates a loss function:
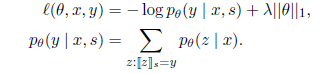
The system will perform a single gradient update using the AdaGrad optimization algorithm (Duchi et al., 2010). This optimization algorithm maintains the perfeature step size.
4. Modeling pragmatics
Based on our experience with the semantic parsing model described in Section 3, we find that the machine has a good learning ability, but lacks the reasoning ability of the human learner. To better illustrate this point of view, we may wish to consider the primary stage of this game. At this stage, θ=0 in the log-linear model pθ(z|x). Assume that humans issue the "red delete" password and treat Zrm-red=remove(with(red)) as the correct logical form. The computer will use the loss function to perform gradient updates, features ("delete", delete) and ("delete", red).
Second, assume that people issue the "remove cyan" password. Note that Zrm-red scores higher than other formulas because ("remove", red) this feature will be used again. Although this behavior is statistically supported, it does not satisfy our instinct for a savvy language learner. In addition, this behavior cannot be applied specifically to our model, but it can be applied to other statistical models that did not accumulate extra knowledge about a specific language before, but try to simply conform to the resulting data. Although we cannot expect the computer to magically guess "remove cyan" as remove (with (cyan)), it can at least reduce the probability of Zrm-ed, because another password has been explained very well and instinctively. Remove red.
Markman and Wachtel (1998) have studied this mutually exclusive phenomenon. They found that in the process of language acquisition, children are ostracized by the second label of an object and viewed it as a label for another brand new thing.
Pragmatic Computers To formally establish mutually exclusive models, we turn to some possible pragmatic models (Golland et al., 2010; Frank & Goodman, 2012; Smith et al., 2013; Goodman & Lassiter, 2015). The model will apply these ideas to the actual operation. Think of language as a cooperative game between the speaker (person) and the listener (computer). During the game, the listener establishes a clear and unambiguous model of the speaker's discourse strategy. This in turn influences the thinking of listeners. This is the core idea of ​​these models. In the canonical computer language, we will define the discourse strategy of the speaker S(z|x) as the discourse strategy of the L(z|x) listener. In the process of communication, the speaker takes into account the semantic semantic analysis model and the speech p(x) from the previous Pθ(z|x). The listener considers the speaker S(z|x) and the previous speech p( z):
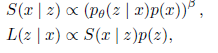
In the above formula, a β≧1 hyperparameter is used to make the normal distribution more uniform (Smith et al., 2013). The computer will use the set and L(z|x) not the set Pθ to rank the game candidates. Note that the pragmatic models we use only affect the ranking of actions performed by humans and do not affect the gradient update of the model.
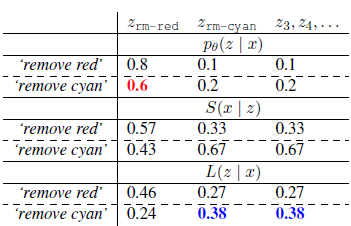
Table 2 assumes that the computer sees an instance "Delete Red" → Zrm-ed and thinks that the "Delete Cyan" command is issued. Above: The literal listener PθZrm-ed incorrectly chose Zrm-ed instead of Zrm-cyan. In the middle: The pragmatic speaker S(x|z) is assigned a higher probability of “removing cyan†based on Zrm-cyan; below: the pragmatic listener L(z|x) is correctly assigned to Zrm-red with a lower probability, Where p(z) is the same.
We use only a simple example to analyze the role of pragmatic modeling. Table 2 shows that when the listener only recognizes the speaker's literal meaning Pθ(zIx), he will give Zrm-red a high probability to respond to the instructions “remove red†and “remove cyanâ€. Assuming that there is a unified, p(x) and β=1 pragmatics, the speaker S(x|z) will maintain normal consistency with each column of Pθ. Note that if pragmatic speakers try to convey Zrm-cyan's message, they are very likely to choose to "remove cyan." Second, assuming constant, the pragmatic listener L(z|x) will maintain normal consistency with each row of Pθ.1. Based on the above assumptions, the following results will be produced: Under the "Delete Cyan" command, Zrm-red speakers will be more likely to choose to communicate Zrm-cyan than to say Zrm-red speakers. And this result square is the ideal effect of the pragmatic model.
Pragmatic listeners set speech as a cooperative communicator, and communicate as much as possible during the exchange process. There are some speaker actions, such as avoiding the use of synonyms (eg, non-“deleting itemsâ€) and using a unified word order (eg, non-red deletes), in violation of game theory. For those speakers who do not follow the discourse strategy, our pragmatic model is not applicable. However, when we get more data in the game, we only understand that the speaker Pθ (z|x) will understand the literal meaning of the speaker. Continuously enhanced, the meaning of the words understood by both the literal speaker and the pragmatic listener will coincide.

Algorithm 1 An online learning algorithm that can update the semantic analysis parameters θ and the total number C, Q requires the computer to perform pragmatic inference.
On-line pragmatic learning In order to implement the pragmatic listener defined in 5, we need to calculate the speaker's normalization constant, ∑xpθ(z|x)p(x) to compute S(x|z)(4). In order to avoid tedious calculation steps on-line, we propose to use Algorithm 1. In this calculation method, an approximate method is used to increase the computational efficiency. First, in order to approximate all the instructions Pθ(x|z), we only calculate the normalization constant ∑xpθ(z|x)p(x)≈∑ipθ(z|xi) by some examples that can be seen. In addition, in order to avoid the repeated use of the existing parameters of each new example to re-parse the previous example, we store the formula Q(z)=∑ipθ(z|xi)β , in which θi is the ith example xi after updating Derived parameters. Although θi is different from the current parameter, for the related example xi, we use the formula pθ(z|xi) ≈pθi(z|xi) to calculate the normalization constant, and the resulting constant values ​​θi and θ represent.
In Algorithm 1, the pragmatic listener L(z|x) can be understood as an important form of the optimized literal listener PθB-, whose importance is reduced by the function Q(z), which reflects the literal Obedients are more inclined to choose what kind of meaning to understand. By building the model, Algorithm 1 is the same as the algorithm mentioned in (4), except that this algorithm uses the normalization constant Q based on the previous parameter θi after referring to the example. According to (5), we also need p(z), which calculates the estimate of p(z) by adding -α to the total number C(z). Note that Q(z) and C(z) are updated when the model parameters corresponding to the current example are updated.
Finally, due to the observation of only the result y of the instruction, rather than the logical form z, the calculation results will present a little complexity. Based on the model C(z)â†C(z)+pθ(z|x,||z||s=y), we simply have each constant logical form {z|||z||s=y} Specify a pseudo code.
Pragmatics has naturally emerged in ILLG compared to the work that previously required pragmatic references. We believe that this form of pragmatics is extremely important in the learning process. However, when we acquire more data, its importance will be reduced. Indeed, when we get a large amount of data and the probability of zs decreases, the following function L(z|x)≈pθ(z|x)as∑xpθ(z|x)p(x)→p(z) will be generated. ), then β=1. However, for semantic analysis, if we can get a lot of data, we will not use this method. In particular, it is worth noting that in the game SHRDLURN, we are far from being able to use this calculation method. Most of our verbal instructions or logical forms can only be seen once, and the importance of the pragmatic model will not be reduced.
5 Experiments
5.1 settings
Data Using the Amazon Turkey Go robot, we paid $3 each for 100 workers and asked them to play SHRDLURN. Starting from the initial state, we have a total of 10,223 verbal instructions. Of course, since the player can perform any action without performing any action, 8874 instructions are marked as instruction y, and the remainder is unmarked. Under the same setting conditions, 100 players completed the entire game. We deliberately make every worker start from scratch in order to study the diversity of strategies under the same control conditions.
Each game consists of 50 tasks, one for each of the 10 tasks, and the total plan is divided into 5 levels. Based on the starting status, an ending is set for each level. Every time a game is completed, it requires an average of 80 instructions. It takes 6 hours to complete the 100 games using the Amazon Turkey Go robot. According to the time tracking device of the Amazon Turkey Go robot, each game will take about 1 hour (this timing method is not suitable for multi-task players). In game control operations, a minimum amount of guidance is provided to these players. It is important that we do not provide example instructions in order to avoid biasing the use of their language. About 20 players are puzzled by the game operation, giving us a lot of useless instruction feedback. Fortunately, most players can understand how to set things up. According to their selective reviews, some players even enjoy SHRDLURN.
That was the most interesting experience I played in the Amazon Turkey Go game.
Wow, this is really the best game!
Indicators We use the number of reels to measure the performance of each player in the game. In each instance, the number of reels is the position on the Y-axis that each player performs. This version of SHRDLURN can be done by reel counting. Twenty-two of the 100 players failed to teach an actual language, but instead completed the game by obtaining the number of reels. We call them spammers, who typically enter single letters, random words, data, or random phrases (eg, "How are you?"). Overall, these junk players get a large number of reels: On average, each instruction gets 21.6 reels, and for non-spammers, they only need 7.4 reels.
5.2 Human Strategy
Some examples of verbal instructions can be found in Table 3. Most players use English, but their language habits are different, such as using definite articles, plural forms, and proper noun ordering. Five players invented their own language. The language of these new inventions is more precise and consistent than ordinary English. One player uses Polish and the other player uses Polish notation (below Table 3).

Table 3: Sample sentences, with the average steps for each player in parentheses. The success of the game is determined by the number of steps, and the number of steps that a successful player will use will be less. (1) The top 20 players prefer to use continuous, concise language whose semantics are very similar to human logical language. (2) Languages ​​used by medium-ranking players are more verbose or discontinuous, which is slightly different from human language patterns. (3) The reasons for the failure vary. Left: Intermediate: Use coordinate system or conjunctions; Right: Begin to be very puzzled, and the language used is far from our logical language.
Overall, we find that players are more comfortable with ILLG games after using continuous, concise and non-repeating language, even though they use standard English at the beginning. For example, some players will become more continuous over time (for example, from using "remove" and "discard" to just using "remove"). In terms of lengthiness, omitting action words is a common adaptation process in games. In the following example taken from different players, we will compare early-appearing sentences with later-appearing sentences: 'Remove the red ones' becomes 'Remove red'; 'add brown on top of red' It became 'add orange on red'; 'add red blocks to all red blocks' became 'add red to red'; 'dark red' became 'red'; the player had spoken in the first 20 sentences. Use 'the' but never seen 'the' in the last 75 sentences.
Players also vary widely in accuracy. Some are too precise (for example, 'remove the orange cube at the left', 'remove red blocks from top row'), and others are not precise or require reading before and after (for example, 'change'. Colors','add one blue','Build more blocus','Move the blocks fool','Add two red cubes'). We have found that over time, players can better understand that ILLG will become more accurate.
The language used by most players does not actually match the logical language in Table 1, and the calculation is a good player. In particular, numbers are used often. Although some concepts are common in the building block world, most are different (for example, 'first block' means 'leftmost'). More specifically, of the top 10 players, 7 use some digital form, and only 3 use the language that exactly matches our logical language. Some players use languages ​​that do not match the logical language of humans, but they perform better. One of the possible explanations is that the required actions will be constrained by logical language or the actions taken will have unexpected explanations. For example, as long as the player only mentions the leftmost or rightmost, the computer can accurately interpret the reference of the numerical position. So if the player says 'rem blk pos 4' and 'rem blk pos 1', the computer can accurately interpret the binary grammar ('pos''1') to the left. On the other hand, the player does not take action or the coordinate system (for example, 'row two column two'), but merely describing the desired state (for example, 'red orange red', '246') will perform poorly. Although the player does not have to use a language that exactly matches the human logic language, partial similarity will certainly help.
Combination. As far as we know, all players use the same combination language; no one uses language that is not related to movement. Interestingly, three players did not space between words. Because we think monosyllabic words are separated by spaces, they must be scrolled many times. (For example, 14.15 said 'orangeonorangerightmost')
5.3 Computer Strategy
We now make a quality assessment of the pace of computer learning, and our learning goal is to achieve high accuracy only by looking at the data at a glance. The number of steps used to evaluate the player is very sensitive to abnormal data, but it is not as intuitive as for accuracy. Instead, we will consider online accuracy as described below. Formally, if the player speaks the T utterance x(j) and marks y(j), then
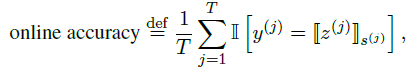
Note that the online accuracy is related to the mark used by the player. If the language used by the player is simple and correct, the mark is in one-to-one correspondence with the actual accuracy. However, it is not suitable for most poor players.
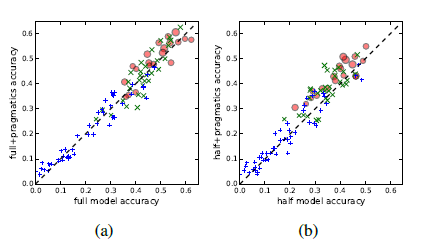
Figure 2: Pragmatics improves online accuracy. In the figure above, each type of tag represents a type of player. Red 0: Indicates the top 20 player's performance in reducing the number of scrolls; Green x: ranked 20-50; Blue +: ranked less than 50 (including poorly performing players). The size of the marker depends on the player's ranking, and the player who performs better has a larger marker. 2a: On-line accuracy with and without pragmatics in full mode; 2b: In semi-complete mode.
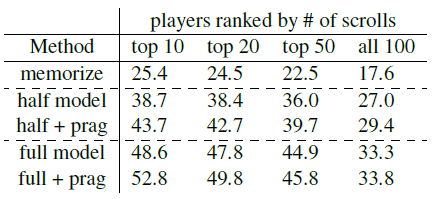
Table 4: Average on-line accuracy for various settings. Storage: characterized by a complete and uncomprehensive logical form; a semi-intact model: expressed in terms of one-, two-, or verb-verbs, but these discourse expressions are logically linked. Full mode: This mode will be described in section 3 +prag: The above mode uses the online semantic algorithm described in section 4. Combinations and pragmatics increase accuracy.
Combination. To study the importance of the combination, we will consider two baselines. First consider the non-combined mode (storage), storing only a few pairs of fully-expressed statements and logic patterns. We use features on feature (x, z) to use index features such as ('remove all the red blocks', zrm-red), in addition to using larger learning rates. Second, we will consider the use of unary, binary, or verb-like features to deal with the semi-complete model of the statement, but its logical model is not combined, so we will have the following characteristics ('remove', zrm-red) , ('red', zrm-red) and so on. Table 4 shows that the full model (section 3) performs significantly better than the storage and semi-baseline models.
Pragmatics. Next we will study the impact of pragmatics on online accuracy. Figure 2 shows that modeling pragmatics is very useful for successful players using simple, continuous language (for example, the player who ranks in the top 10 in terms of scrolling). Interestingly, pragmatic modeling is not helpful or even harmful for players who use inaccurate or discontinuous languages. This is the expected behavior: Pragmatic modeling assumes that human performance is cooperative and rational. For the lower ranked player, this assumption is not valid, because pragmatic modeling in this case is not helpful.
6. Related work and discussion
Our research work will be linked to the related work of a large number of "landing" languages, because in some cases language is a way to achieve some goals. Examples include playing games, interacting with robots, and obeying instructions; we use semantics to logically analyze discourse, which is critical in these settings.
The use of new interactive learning in language games (ILLG) is unique to our research. In this setting, patterns must shift from catching learning to interactive learning. Although online gradient descent is often used, for example, in semantic analysis, we will use online gradient descent in real online settings, skipping in the data and making online accuracy measurements.
In order to increase the learning rate, we will use pragmatic calculation models. The main difference is that previous studies have been based on pragmatics using a trained basic model, but we will learn the online model. Monore and Potts learn to improve pragmatics. In contrast, we use pragmatics to accelerate the learning process by capturing phenomena like mutual exclusion. We differ from previous research in some minor details. First, we perform pragmatic modeling under online learning settings, and we also update the pragmatics model online. Second, reference games are unlikely to play a crucial role through design. Shrdlurn does not specifically design in accordance with the required pragmatics. The improvements we have achieved are all due to players trying to use a consistent language. Finally, we will regard discourse and logic patterns as features of a combinational goal. Smith et al. classify utterances (eg, words) and logical forms (eg, goals); Monroe and Potts use features but also cover the average category.
In the future, we believe that the ILLG setup will be worth studying and have important implications for natural language interfaces. Today, these systems were trained and deployed. If, in this study, these systems can quickly adapt to the user's real-time feedback, we may be able to create a more stable system for resource-poor languages ​​and new areas, but this system is customized and can improve performance through the use of .
Comments from Associate Professor Li Yanjie of Harbin Institute of Technology: This article uses a new interactive learning method to study language game problems. The paper analyzes human strategies and finds that using semantic synthesis and avoiding synonyms is positively related to task performance; comparing computer strategies, The discovery of modeled pragmatics based on semantic analysis models can accelerate the learning process for more strategic players. Compared with the previous methods, the main difference in this paper is that this paper adopts a new interactive learning method. Through the interactive model, language can be learned from clutter. In order to increase the learning rate, the thesis makes use of pragmatic calculation models and can learn models online. Using pragmatics to capture mutually exclusive phenomena accelerates the learning process.
PS : This article was compiled by Lei Feng Network (search “Lei Feng Network†public number) and it was compiled without permission. More ACL related information Scan code Focus on WeChat group