Introduction to Gaussian Filtering, Gaussian Filtering Properties and Applications

1. Introduction to Gaussian filtering

Before we understand Gaussian filtering, we first familiarize ourselves with Gaussian noise. Gaussian noise refers to a type of noise whose probability density function obeys a Gaussian distribution (ie, a normal distribution). If a noise whose amplitude distribution obeys Gaussian distribution and its power spectral density is evenly distributed, it is called Gaussian white noise. The second moment of Gaussian white noise is irrelevant, and the first moment is a constant, which refers to the temporal correlation of successive signals. Gaussian white noise includes thermal noise and shot noise.

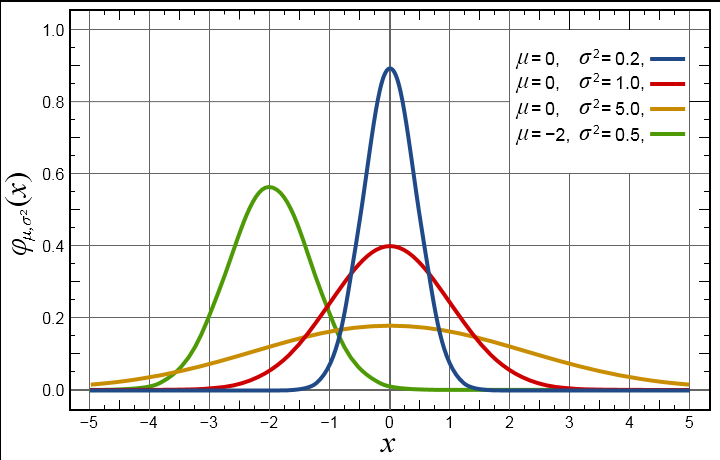
A Gaussian filter is a type of linear smoothing filter that selects a weight according to the shape of a Gaussian function. The Gaussian smoothing filter is very effective for suppressing noise that is normally distributed. The one-dimensional zero-mean Gaussian function is:

g(x)=exp( -x^2/(2 sigma^2)

Among them, the Gaussian distribution parameter Sigma determines the width of the Gaussian function. For image processing, two-dimensional zero-mean discrete Gaussian functions are commonly used as smoothing filters and Gaussian functions:

2, Gaussian filter function

For images, a Gaussian filter is a 2-dimensional convolution operator that uses a Gaussian kernel for image blurring (removing details and noise).

1) Gaussian distribution

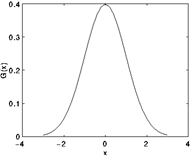
One-dimensional Gaussian distribution:

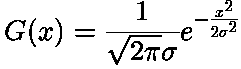
Two-dimensional Gaussian distribution:

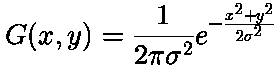
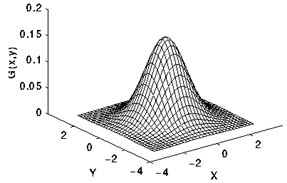
2) Gaussian nuclear

In theory, the Gaussian distribution has non-negative values ​​over all defined domains. This requires an infinitely large convolution kernel. In fact, you only need to take the value within 3 times the standard deviation around the mean, and the other parts can be removed directly. The following figure shows an integer Gaussian kernel with a standard deviation of 1.0.

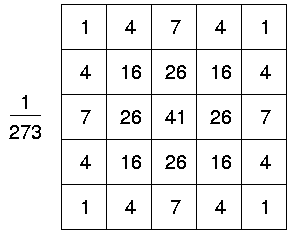
3, Gaussian filter property

The Gaussian function has five important properties that make it particularly useful in early image processing. These properties indicate that the Gaussian smoothing filter is a very effective low-pass filter both in the spatial domain and in the frequency domain, and has been effectively used by engineers in actual image processing. Gaussian functions have five very important properties. They are:

(1) The two-dimensional Gaussian function has rotational symmetry, that is, the smoothness of the filter in all directions is the same. In general, the direction of the edge of an image is not known in advance, and therefore, it cannot be determined before filtering that one direction needs more smoothing than the other direction. Rotational symmetry means that the Gaussian smoothing filter will not be biased in either direction in subsequent edge detection.

(2) Gaussian functions are single-valued functions. This shows that the Gaussian filter replaces the pixel value of the point with the weighted mean of the neighborhood of the pixel, and the weight of each neighboring pixel point monotonically increases or decreases with the distance from the point to the center point. This property is important because the edge is a local feature of the image. If the smoothing operation still has a large effect on the pixels far from the center of the operator, the smoothing operation will distort the image.

(3) The Fourier transform spectrum of the Gaussian function is single-lobed. As shown below, this property is a direct corollary to the fact that the Gaussian function Fourier transform is equal to the Gaussian function itself. Images are often contaminated with unwanted high-frequency signals (noise and fine texture). The desired image features (eg, edges) contain both low frequency components and high frequency components. The single lobe of the Fourier transform of the Gaussian function means that the smooth image is not contaminated by undesired high-frequency signals while retaining most of the desired signal.

(4) The width of the Gaussian filter (determining the degree of smoothness) is characterized by the parameter σ, and the relationship between σ and the degree of smoothness is very simple. The larger σ is, the wider the frequency band of the Gaussian filter is, and the smoother the better. By adjusting the smoothness parameter [sigma], a trade-off can be made between excessively blurred (over-smoothed) image features and excessive undesired abrupt changes (under-smoothing) due to noise and fine texture in smooth images.

(5) Due to the separability of the Gaussian function, a larger Gaussian filter can be effectively implemented. A two-dimensional Gaussian function convolution can be performed in two steps. First, the image is convolved with a one-dimensional Gaussian function, and then the convolution result is convolved with the same one-dimensional Gaussian function that is perpendicular to the direction. Therefore, the computational complexity of two-dimensional Gaussian filtering increases linearly with the width of the filter template rather than squared.

4, Gaussian filter application

The degree to which the Gaussian filtered image is smoothed depends on the standard deviation. Its output is the weighted average of the pixels of the domain, and the higher the weight of pixels that are closer to the center. Therefore, it has a smoother effect with respect to the mean filter and preserves edges better.

The essential reason why Gaussian filtering is used as a smoothing filter is because it is a low-pass filter, see the figure below. Moreover, most of the convolution-based smoothing filters are low-pass filters.

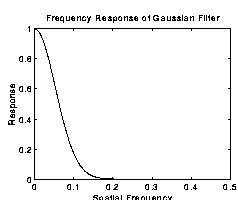
Figure: Frequency response of a Gaussian filter (standard deviation = 3 pixels). The spatial frequency axis is marked in cycles per pixel, and hence no value above 0.5 has a real meaning.

5, Gaussian filtering steps

(1) Move the central element of the relevant core so that it is directly above the pixels to be processed in the input image

(2) Multiply the pixel value of the input image by the relevant core

(3) Add the results obtained in the above steps as output

6, Gaussian filtering source code (C language version) (click to read the original to view the source code)

After Gaussian filtering:

Before Gaussian filtering:

Beam Light

1).Excellent pattern,mute,the best effect of the light is 5 to 30 meters.

2).Competitive price and high quality.

3).LCD Chinese and English bilingual menu,brightness.

4).Suitable for performances,bars,banquet hall,multi-purpose conference room,theater,studio,etc.

Our company have 13 years experience of LED Display and Stage Lights , our company mainly produce Indoor Rental LED Display, Outdoor Rental LED Display, Transparent LED Display,Indoor Fixed Indoor LED Display, Outdoor Fixed LED Display, Poster LED Display , Dance LED Display ... In additional, we also produce stage lights, such as beam lights Series, moving head lights Series, LED Par Light Series and son on...

Beam Light Series,Sharpy Beam Light,Led Moving Beam Head Light,Led Beam Light

Guangzhou Chengwen Photoelectric Technology co.,ltd , https://www.cwledpanel.com