ReLU to Sinc's 26 neural network activation functions to visualize large inventory

In a neural network, an activation function determines the output of a node from a given input set, where the nonlinear activation function allows the network to replicate complex nonlinear behavior. Just as most neural networks are optimized with some form of gradient descent, the activation function needs to be differentiateable (or at least almost completely differentiable). In addition, complex activation functions may cause some gradients to disappear or explode. Therefore, neural networks tend to deploy several specific activation functions (idenTIty, sigmoid, ReLU, and their variants).

Below is a graphical representation of the 26 activation functions and their first derivative. On the right side of the diagram are some properties related to the neural network.

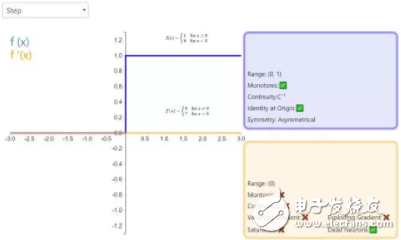
The activation function Step is more theoretical rather than practical, and it mimics the properties of biological neurons that are either all or none. It cannot be applied to neural networks because its derivative is 0 (except for the zero derivative is not defined), which means that gradient-based optimization is not feasible.

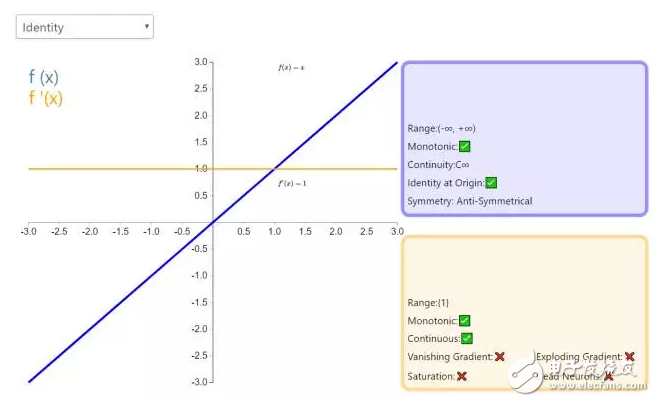
By activating the function IdenTIty, the input of the node is equal to the output. It is perfect for tasks where the underlying behavior is linear (similar to linear regression). When there is nonlinearity, it is not enough to use the activation function alone, but it can still be used as an activation function for the regression task on the final output node.

All In One Portable Solar Power System

All In One Portable Solar Power System,All In One Solar Generator,Max Portable Solar Power Generator,Portable Solar Panel Array

Shenzhen Sunbeam New Energy Co., Ltd , https://www.sunbeambattery.com