What is the difference between a floating point processor and a fixed point processor?
The C2000 microprocessor of the C28x+FPU architecture adds some registers and instructions to the original C28x fixed-point CPU to support IEEE single-precision floating-point operations. For programs written on fixed-point microprocessors, the floating-point C2000 is also fully compatible and does not require changes to the program. Floating point processors have the following advantages over fixed point processors:
Programming is simpler
Better performance, such as division, square root, FFT and IIR filtering algorithms are more efficient.
The program is more robust.
First, the floating point number of IEEE754 format
The single precision floating point number of C28x+FPU follows the IEEE754 format. it includes:
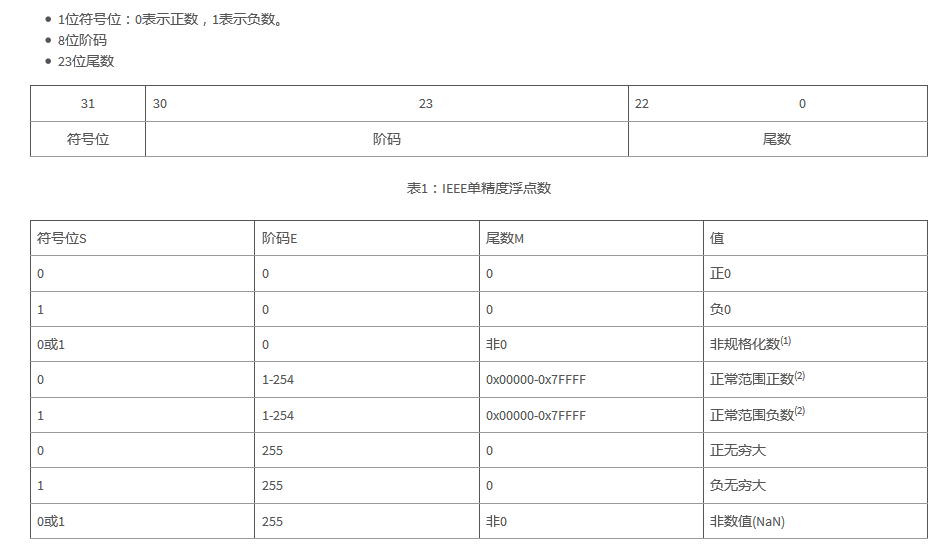
mantissa
Table 1: IEEE single-precision floating-point numbers
(1) The denormalized value is very small, and the calculation formula is (-1) sx2(E-126)x0.M
(2) The normal range numerical formula is (-1) sx2(E-127)x1.M
The normal range values ​​fall within the range of ± ~ 1.7 x 10 -38 to ± 3.4 x 10 +38. As can be seen from Table 1, the IEEE754 standard includes:
Standard data formats and special values ​​such as non-numeric (NaN) and infinity
Standard rounding mode and floating point arithmetic
Multi-platform support, including the Texas Instruments C67x family of chips.
The C2000 made some simplifications to the standard:
Status flags and comparison operations do not distinguish between positive 0 and negative 0
The denormalized value is considered to be 0
Non-numeric (NaN) processing is the same as infinity.
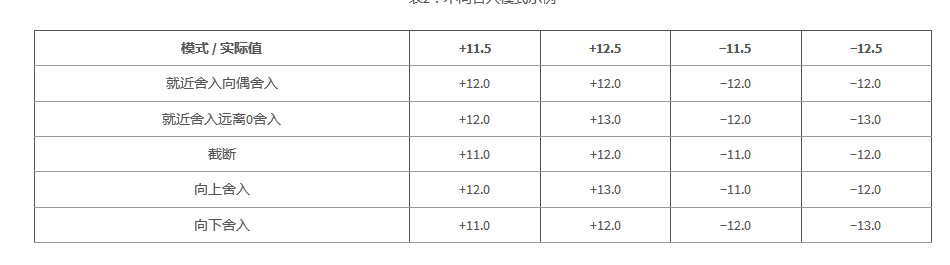
The IEEE754 standard has five rounding modes, and the C28x+FPU only supports two of them:
- truncation: decimal places are all rounded off regardless of size
- Rounding down to the nearest round: In this mode, if the decimal place is less than 5, it is rounded off, if it is greater than 5, it is rounded. If the decimal place is 5, it is rounded to the nearest even number.
Table 2 shows the impact of different rounding modes on the data. By default, the C28x+FPU compiler configures the microprocessor to be rounded to the even rounding mode [1].
Table 2: Examples of different rounding modes
Second, floating point C2000 chip computing skills and points of attention
The precision of floating-point numbers is determined by the mantissa bits. Most of the numbers have errors when expressed in floating-point numbers. These errors are small and can be ignored in most cases. However, after many calculations, the error may be unacceptable. .
The following example is used to illustrate. The following code defines the float type variable, which is 11.7 plus 20001 on CPU1 and CLA1 of TI's latest Delfino chip F28379D.
Float CLATMPDATA=0;
Int index=20001;
While (index--)
{
CLATMPDATA=CLATMPDATA+11.7;
}
The following results were obtained:
Among them, CLATMPDATA1 is the result obtained by adding 11.7 to 20001 times in CLA, and CLATMPDATA2 is the result obtained by adding 11.7 to 20001 times in the CPU. It can be seen that the results obtained by the two are different, and both have a large gap with the correct result 234011.7.
Why are CPU and CLA calculations different?
The difference between the CPU and CLA results is due to the difference in the rounding mode of the floating point numbers. As mentioned earlier, the C28x+FPU compiler configures the CPU to be rounded to the even rounding mode by default. Unlike CLA, CLA defaults to truncated rounding mode [2]. In the CLA code, we can add the following code:
__asm(" MSETFLG RNDF32=1"); //1 is rounded to nearest rounding, 0 is truncated rounding
Change the rounding mode of the CLA to the nearest rounded to even rounding mode, and then run the code to get the same result as the CPU.
2. Why are there large errors in CPU and CLA calculations? How to solve?
11.7 is 0x413b3333 when expressed in floating point number of IEEE754 format, and its corresponding actual value is 11.69999980926513671875. It can be seen that the error is small, but after multiple times of rounding and multiple rounding, the result is larger. For this, we can Define CLATMPDATA as a long double variable (64 bits), run the same code again, you can get the following results, you can see that the error is small and can be ignored.
It should be noted that the existing C28x CPU only supports single-precision (32-bit) hardware floating-point operations. The operation of 64-bit double-precision floating-point numbers is implemented by software, so the operation rate will be much slower. In addition, CLA does not support 64 digits.
In this example, we can observe the assembly code of the float type variable and the long double type variable separately as follows:
C code: CLATMPDATA2=CLATMPDATA2+11.7;
If CLATMPDATA2 is a float variable, the corresponding assembly code is:
00c08d: E80209D8 MOVIZ R0, #0x413b 1cycle
00c08f: E2AF0112 MOV32 R1H, @0x12, UNCF 1cycle
00c091: E8099998 MOVXI R0H, #0x3333 1cycle
00c093: E7100040 ADDF32 R0H, R0H, R1H 2cycle
00c095: 7700 NOP 1cycle
00c096: E2030012 MOV32 @0x12, R0H 1cycle
If CLATMPDATA2 is a long double variable, the corresponding assembly code is:
00c08b: 7680005A MOVL XAR6, #0x00005a 1cycle
00c08d: 8F00005A MOVL XAR4, #0x00005a 1cycle
00c08f: 8F40C26A MOVL XAR5, #0x00c26a 1cycle
00c091: FF69 SPM #0 1cycle
00c092: 7640C0C9 LCR FD$$ADD 4cycle (time to jump)
+25cycle (the FD$$ADD function requires 25 cycles internally)
It can be seen that it takes 7 cycles for the CPU to perform an addition to the float type, and 33 cycles for the addition of the long double type.
Â
Third, the conclusion
1. The C2000's CPU and CLA default rounding mode are different. You may get different results when calculating floating point numbers, but we can change the rounding mode by code to get the same result.
2. Single-precision floating-point numbers may have large errors after multiple calculations. You can solve the accuracy problem by defining the variable as a 64-bit long double.
3. The C28x CPU only supports single-precision (32-bit) hardware floating-point operations. The operation of 64-bit double-precision floating-point numbers is implemented by software, so the operation rate will be much slower. In the next generation of C2000 products we will implement hardware support for 64-bit double-precision floating-point arithmetic.
A waterproof slip ring is a type of sealant that can be used to create a watertight seal between two surfaces. This seal can be used in a variety of applications, including plumbing and automotive manufacturing. Waterproof slip rings are often used in conjunction with other types of seals to create a watertight system. It enables liquid and gas to flow freely between the two, without any leakage. This essential technology is used in a variety of industries, from automotive manufacturing to food processing.
Waterproof slip rings are mainly made of silicone rubber. They can be used in harsh environments and have a long life span. Silicon is an inert material and does not corrode in water or other liquids. It also has a low coefficient of friction, which makes it ideal for use in moving parts. Slip ring motors are typically used in high-power applications where large amounts of the current need to be transmitted. They are made of copper or aluminum to provide good electrical conductivity.
The Oubaibo waterproof slip ring is very popular on the market. It is made of high-quality materials and has a long lifespan. The slip ring is also very easy to use, and it can be connected to a wide range of devices. Additionally, the slip ring is Ethernet-enabled, which makes it perfect for industrial applications.
Waterproof Slip Ring,Slip Ring Motor Application,Electrical Slip Rings Industrial,Slip Rings Ethernet
Dongguan Oubaibo Technology Co., Ltd. , https://www.sliprobs.com